论文: https://arxiv.org/pdf/2110.02178.pdf
代码: https://github.com/chinhsuanwu/mobilevit-pytorch/blob/master/mobilevit.py
轻量级卷积神经网络（CNN）在移动视觉任务中具有主导地位，但缺乏全局信息建模能力。相比之下，基于自注意力的视觉transformer（ViT）能学习全局表示，但参数量大且优化困难。很容易想到将CNN和ViT相结合，这篇文章就是这么干的。所以从设计上并没有什么特殊的，属于那种很容易想到的点子，但是很容易想到的点子实验效果不一定好，所以这篇文章还是有价值的。
常规结构
因为想法很简单，这篇就直接介绍模型结构吧！
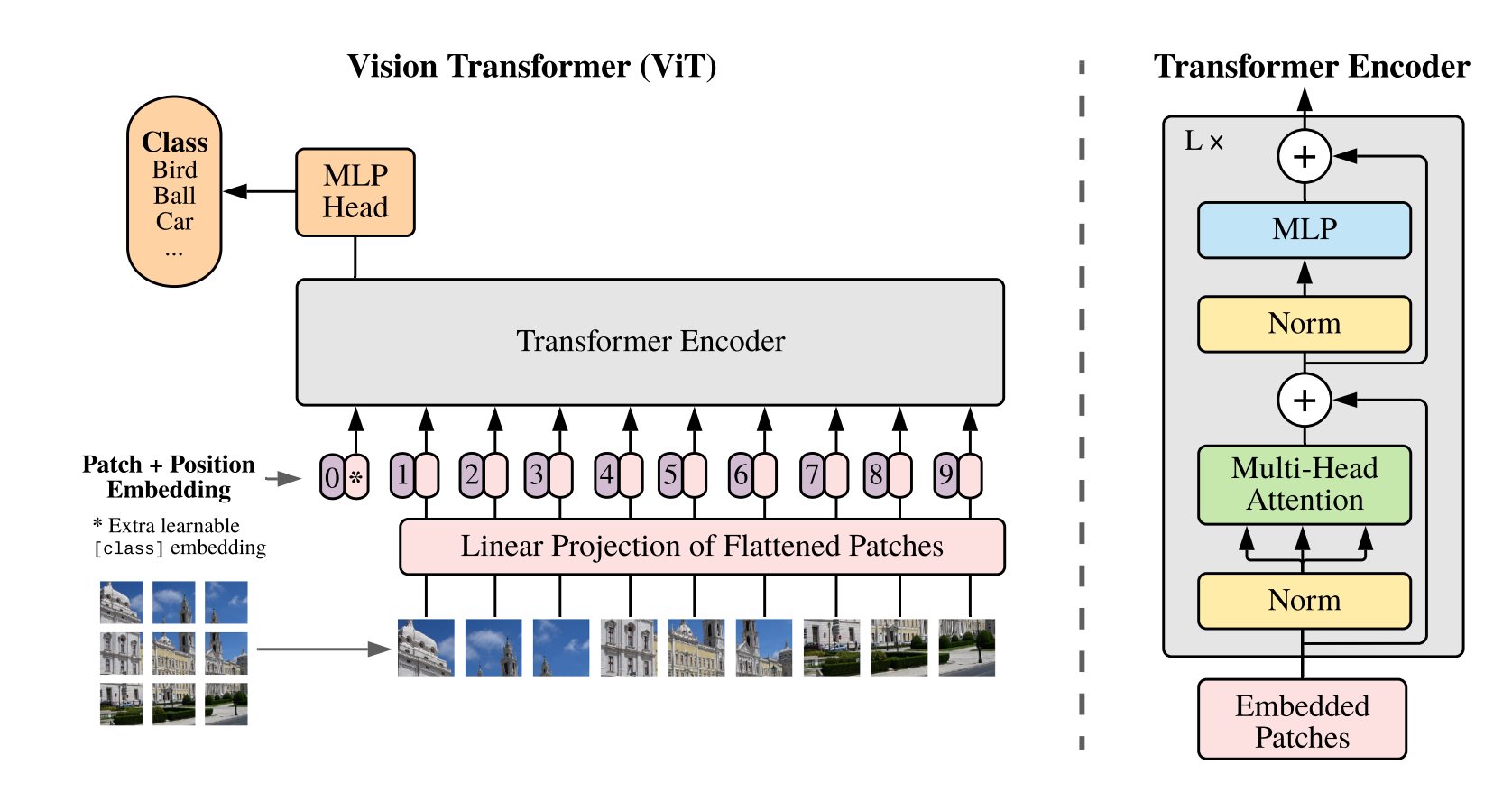
一般的ViT结构就是上图，先把原图切分成patch，比如假设图像大小为$224\times224\times3$，切分成$16\times 16$的块，一共会得到$14\times14=196$个块。
原始输入图片通道为RGB，所以通道数为3，每个patch的特征维度也就是：$16\times16\times3=768$。所以一张图片现在可以表达成$196\times768$的特征。一般来说，会用一个全连接把768这个维度变换一下，比如由$196\times768$变成$196\times256$，Transformer会把196视为token数目，256视为每个token的特征维度，然后加入位置信息进行建模。
但是这种机构依赖力大砖飞，需要参数量和训练数据量都搞上去了，模型效果才有提升。原因就是缺少空间归纳偏置，所谓空间归纳偏置简单来说：卷积层是利用局部像素信息来提取图像特征，而不是通过全局信息。这种偏置有助于神经网络更有效地学习图像特征，因为它模拟了人类视觉系统中的局部处理机制。相比之下，ViT直接通过自注意力机制学习全局表示，因此缺乏这种空间偏置。
好家伙，这句话不就是说其实卷积神经网络的建模方式更合理嘛！那要transformer这种全局建模干嘛？
但是成年人没非此即彼的二元对立的，只有比例问题，我这么说感觉更好接受一点：那就是空间归纳偏置在一定程度上是比较符合建模方式的，它其实也是transfomer的子集，只要参数量和计算量上来了，transformer也能够学到一个合理的空间归纳偏置，它可能还会比卷积神经网络这种人为定义的空间计算方式更优。所以我们可以先给模型一点空间归纳偏置，但是呢也给它一点全局建模的自由度，就像和面时候的面粉与水的比例一样，只有比例对了，参数量和模型准确度都能更优。
本文结构
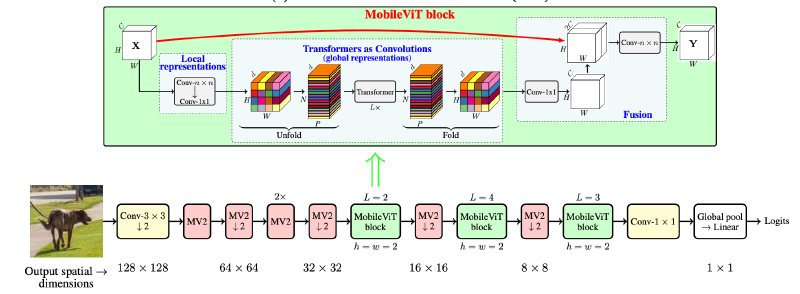
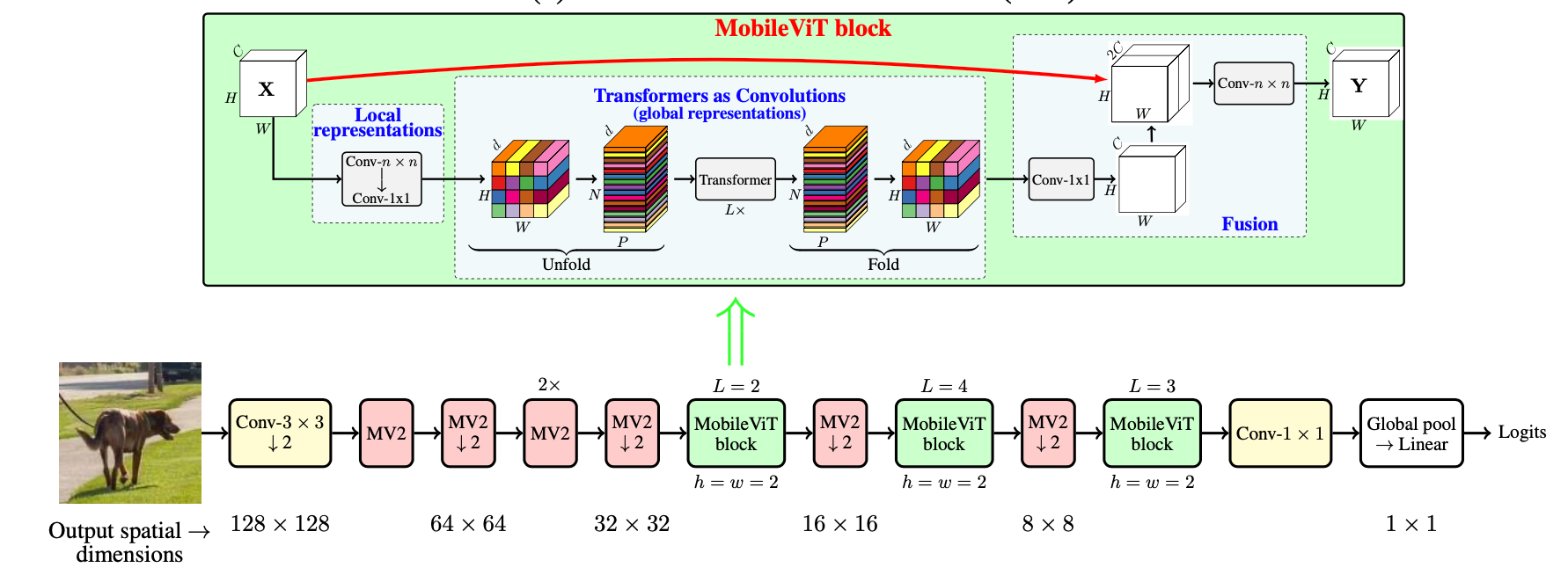
上面已经说了，本文就是把卷积层和transformer给结合起来。下面的MV2其实就是MobileNetV2中的块，加了下划线的代表进行了几倍下采样。
那就先从熟悉的开始吧，先看MV2的代码。其实就是深度可分离卷积，先depth-wise卷积再point-wise卷积。
expansion这个参数就是要不要弄成漏斗结构，先把输入维度用point-wise映射为隐藏层维度，漏斗结构的隐藏层维度要大于输入特征维度，然后再进行深度可分离卷积映射为输出维度，输出维度也是小于隐藏层维度的。这种先变胖再变瘦的漏斗结构其实就是MobileNetV2的一个创新点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class MV2Block(nn.Module):
def __init__(self, inp, oup, stride=1, expansion=4):
super().__init__()
self.stride = stride
assert stride in [1, 2]
hidden_dim = int(inp * expansion)
self.use_res_connect = self.stride == 1 and inp == oup
if expansion == 1:
self.conv = nn.Sequential(
# dw
nn.Conv2d(hidden_dim, hidden_dim, 3, stride, 1, groups=hidden_dim, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.SiLU(),
# pw-linear
nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
nn.BatchNorm2d(oup),
)
else:
self.conv = nn.Sequential(
# pw
nn.Conv2d(inp, hidden_dim, 1, 1, 0, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.SiLU(),
# dw
nn.Conv2d(hidden_dim, hidden_dim, 3, stride, 1, groups=hidden_dim, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.SiLU(),
# pw-linear
nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
nn.BatchNorm2d(oup),
)
def forward(self, x):
if self.use_res_connect:
return x + self.conv(x)
else:
return self.conv(x)
|
整个MobileViT先用几个MV2进行了局部信息提取，然后再上MobileViT block来进行全局信息建模。这块也很简单,先用一个$n \times n$的普通卷积，再接着一个$1\times1$的普通卷积，中间是transfomer块，结尾是先用$1\times1$的普通卷积，再用$n \times n$的普通卷积，不过我也不知道作者为什么这么搞，干嘛不就是开头结尾都用一个$n\times n$的普通卷积搞定，可能就是随便弄的吧，毕竟实验部分也没讲这块。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class MobileViTBlock(nn.Module):
def __init__(self, dim, depth, channel, kernel_size, patch_size, mlp_dim, dropout=0.):
super().__init__()
self.ph, self.pw = patch_size
self.conv1 = conv_nxn_bn(channel, channel, kernel_size)
self.conv2 = conv_1x1_bn(channel, dim)
self.transformer = Transformer(dim, depth, 4, 8, mlp_dim, dropout)
self.conv3 = conv_1x1_bn(dim, channel)
self.conv4 = conv_nxn_bn(2 * channel, channel, kernel_size)
def forward(self, x):
y = x.clone()
# Local representations
x = self.conv1(x)
x = self.conv2(x)
# Global representations
_, _, h, w = x.shape
x = rearrange(x, 'b d (h ph) (w pw) -> b (ph pw) (h w) d', ph=self.ph, pw=self.pw)
x = self.transformer(x)
x = rearrange(x, 'b (ph pw) (h w) d -> b d (h ph) (w pw)', h=h//self.ph, w=w//self.pw, ph=self.ph, pw=self.pw)
# Fusion
x = self.conv3(x)
x = torch.cat((x, y), 1)
x = self.conv4(x)
return x
def conv_1x1_bn(inp, oup):
return nn.Sequential(
nn.Conv2d(inp, oup, 1, 1, 0, bias=False),
nn.BatchNorm2d(oup),
nn.SiLU()
)
def conv_nxn_bn(inp, oup, kernal_size=3, stride=1):
return nn.Sequential(
nn.Conv2d(inp, oup, kernal_size, stride, 1, bias=False),
nn.BatchNorm2d(oup),
nn.SiLU()
)
|
Transformer定义如下，也比较简单，也就是注意力层加前馈层，不管是注意力层还是前馈层用的都是prenorm，也就是先做layer norm，再做其他运算，而不是做完了其他运算再做layer norm。特别值得注意的是，这里的transformer竟然把位置编码给去掉了，所以MobileViT是没有位置编码的！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
super().__init__()
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(nn.ModuleList([
PreNorm(dim, Attention(dim, heads, dim_head, dropout)),
PreNorm(dim, FeedForward(dim, mlp_dim, dropout))
]))
def forward(self, x):
for attn, ff in self.layers:
x = attn(x) + x
x = ff(x) + x
return x
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout=0.):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, hidden_dim),
nn.SiLU(),
nn.Dropout(dropout),
nn.Linear(hidden_dim, dim),
nn.Dropout(dropout)
)
def forward(self, x):
return self.net(x)
class Attention(nn.Module):
def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
super().__init__()
inner_dim = dim_head * heads
project_out = not (heads == 1 and dim_head == dim)
self.heads = heads
self.scale = dim_head ** -0.5
self.attend = nn.Softmax(dim = -1)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)
self.to_out = nn.Sequential(
nn.Linear(inner_dim, dim),
nn.Dropout(dropout)
) if project_out else nn.Identity()
def forward(self, x):
qkv = self.to_qkv(x).chunk(3, dim=-1)
q, k, v = map(lambda t: rearrange(t, 'b p n (h d) -> b p h n d', h = self.heads), qkv)
dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale
attn = self.attend(dots)
out = torch.matmul(attn, v)
out = rearrange(out, 'b p h n d -> b p n (h d)')
return self.to_out(out)
|
多分辨率采样器
基于ViT的模型中学习多尺度表示的标准方法是微调，因为位置嵌入需要根据输入尺寸进行插值，如果输入图片尺寸变大，patch大小不变，那么token会变长，计算速度会显著变慢。那你一定想到，那就直接改变patch尺寸呗，维持patch数量不变，但对于普通的ViT这是不行的。
为什么不行呢？CNN是因为池化层导致了它有一定的尺度不变性，但普通ViT不行，因为ViT是全连接神经网络，全连接层压根就没有尺度不变性，它只会处理固定尺寸大小，比如训练的pathc大小为$16\times16$,那推理也要用这个尺寸。
但是MobileViT没有这个问题，它是可以变分辨率输入的，这是因为MobileViT里面有CNN，CNN有尺度不变性，反正不管对于什么尺寸的输入，全给切分为相同数量的patch。
所以训练的时候，MobileViT就输入了不同大小的图片，从而支持它对于不同分辨率输入的效果。给定一系列分辨率$S={(H_1,W_1),…,(H_n,W_n)}$,对应的最大输入分辨率$H_n,W_n$来说，它的batch size为$b$。因为是多卡训练，每个GPU上可以分配不同的分辨率图片，对于某个GPU而言，它的batch size为$b_t=H_nW_nb/H_t/W_t$。其实就是对于小尺寸的图像用大的batch size，大尺寸的图像用小的batch size，避免对GPU内存的浪费，这一块的实现需要自己写一个数据集的sampler，论文有提供可以看看。
多分辨率输入也提高了模型泛化性，比如说验证集loss会更低，同时在不同尺寸上的精度效果也更好。
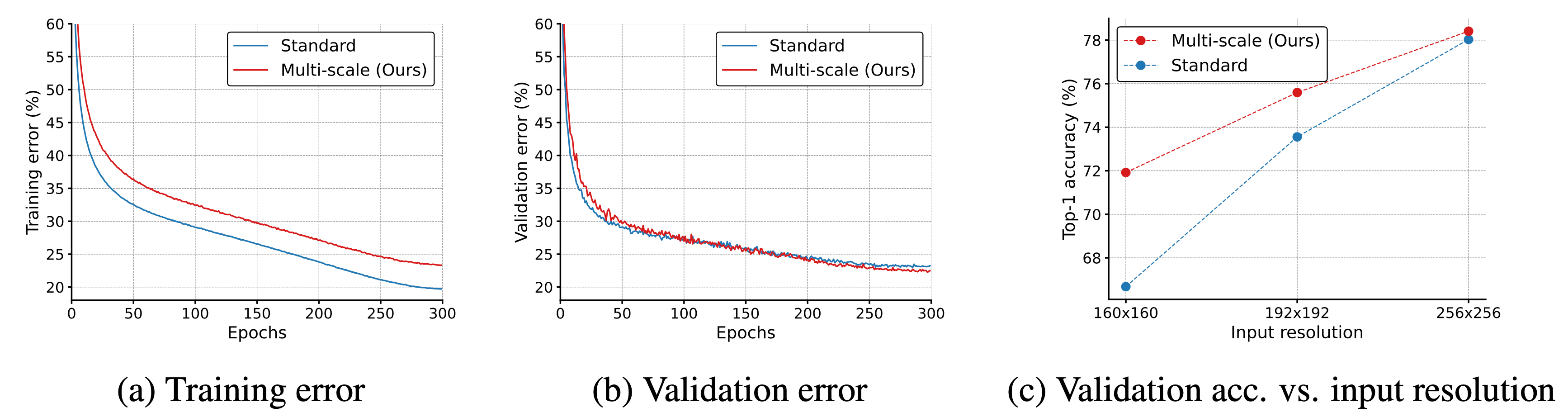这个方法不仅对于这篇文章可以用，对于CNN也是可以用的，比如作者就把他用在了ResNet和MobileNetV2上，发现测试精度也提高了，所以我们也可以用上这个trick，毕竟无痛长了一个多点。
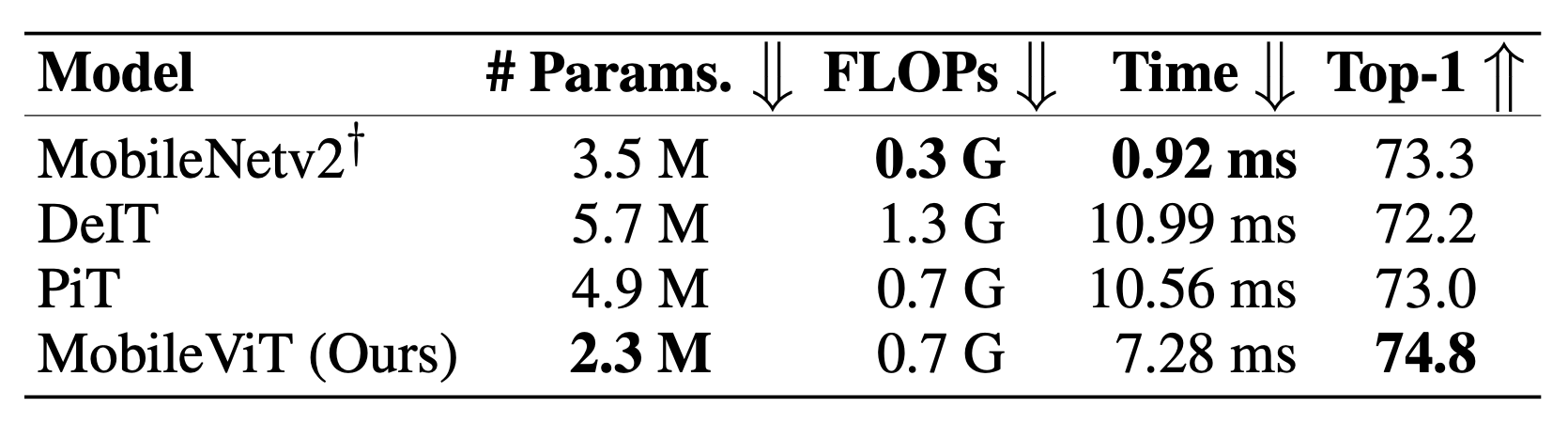
效果
虽然说参数少了，模型Top1精度也高了，但是MobileViT的推理速度在移动设备上是比不过MobileNetV2的，我觉得这是正常的，因为前者计算量Flops是后者的两倍多，但是即使如此，速度慢八倍也不合理。这可能是因为CNN的优化比较多，比如CNN可以把卷积和BN层在推理的时候可以融合为一层(吸BN)，这能够改善内存访问，加快推理速度。
