先按照顺序列一下这几篇技术首次提交到arxiv的时间，我们按照提交时间来介绍，很多博客都搞不清楚发表时间，甚至把这几种方法张冠李戴，我们还是从原始信息源头进行梳理，这样虽然慢但是可靠。

论文：Adapter: Parameter-Efficient Transfer Learning for NLP 代码：Adapter 时间：2019.2.2

论文：Prefix-Tuning: Optimizing Continuous Prompts for Generation 代码：Prefix-Tuning 时间：2021.01.01

论文：P-tuning: GPT Understands, Too 代码：P-Tuning 时间：2021.03.18

论文：The Power of Scale for Parameter-Efficient Prompt Tuning 代码：Prompt Tuning 时间：2021.4.18

论文：LoRA: Low-Rank Adaptation of Large Language Models 代码：Lora 时间：2021.06.17

论文：BitFit: Simple Parameter-efficient Fine-tuning for Transformer-based Masked Language-models 代码：BitFit 时间：2021.06.18

论文：P-Tuning v2: Prompt Tuning Can Be Comparable to Fine-tuning Universally Across Scales and Tasks 代码：P-Tuning v2 时间：2021.10.14

论文：T-Few: Few-Shot Parameter-Efficient Fine-Tuning is Better and Cheaper than In-Context Learning 代码：T-Few 时间：2022.04.11

BitFit从首次提交Arxiv时间来比，要比LoRA晚一天，但是LoRA在论文中对比了BitFit，所以从完成时间上看，BitFit应该比LoRA早。用一句话来概括，BitFit微调的就是模型的偏置项，这有点意思，LoRA微调的是权重，而BitFit微调的是偏置。

具体来说，一个LLM包含$L$层，具体到第$l$层有$M$个自注意力头，用$(m,l)$来代表第$l$层的第$m$个注意力头，它里面有key，query，value这四个编码器，每个都是一个线性层，可以表示为： $$ Q^{m,l}(x)=W_q^{m,l}x+b_q^{m,l} $$

$$ K^{m,l}(x)=W_k^{m,l}x+b_k^{m,l} $$

$$ V^{m,l}(x)=W_v^{m,l}x+b_v^{m,l} $$

这里$x$是上一层transformer层的输出，key，query，value之后通过注意力机制来得到参数$h_1^l$，注意这里的1不是指的第一层，只是作者后面还要用到$h_2^l$，$h_3^l$，用来区分变量的下标而已，没什么特殊含义。

$$ h_1^l=attn(Q^{1,l},K^{m,l},V^{1,l},…,Q^{m,l},K^{m,l},V^{m,l}) $$

这一步就是用了下面的注意力公式，没有任何可学习参数。

$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) V $$

再接着是喂到带有layer-norm的前馈层，一系列的运算如下： $$ h_2^l=Dropout(W_{m_1}^l·h_1^l+b_{m_1}^l) $$

$$ h_3^l=g_{LN_1}^l \odot \frac {(h_2^l+x)-\mu} \sigma+b_{LN_1}^l $$

$$ h_4^l=GELU(W_{m_2}^l·h_3^l+b_{m_2}^l) $$

$$ h_5^l=Dropout(W_{m_3}^l·h_4^l+b_{m_3}^l) $$

$$ out^l=g_{LN_2}^l \odot \frac {(h_5^l+h_3^l)-\mu} \sigma+b_{LN_2}^l $$

这里所有的$b$都是偏置项，它们占全体参数的比例很小，本文证明了可以冻结$W,g$，仅仅微调$b$就能获得一个不错的效果。同时本文还进行了实验，证明不需要微调所有的偏置，仅仅微调query层和第二个全连接层里面的偏置（也就是$b_q^{(·)}$和$b_{m2}^{(·)}$）也能收获相当的效果。

实验

从实验结果上看，本文方法要比Adapter要好，尽管学习参数只有前者的1/45，但是效果却更好。

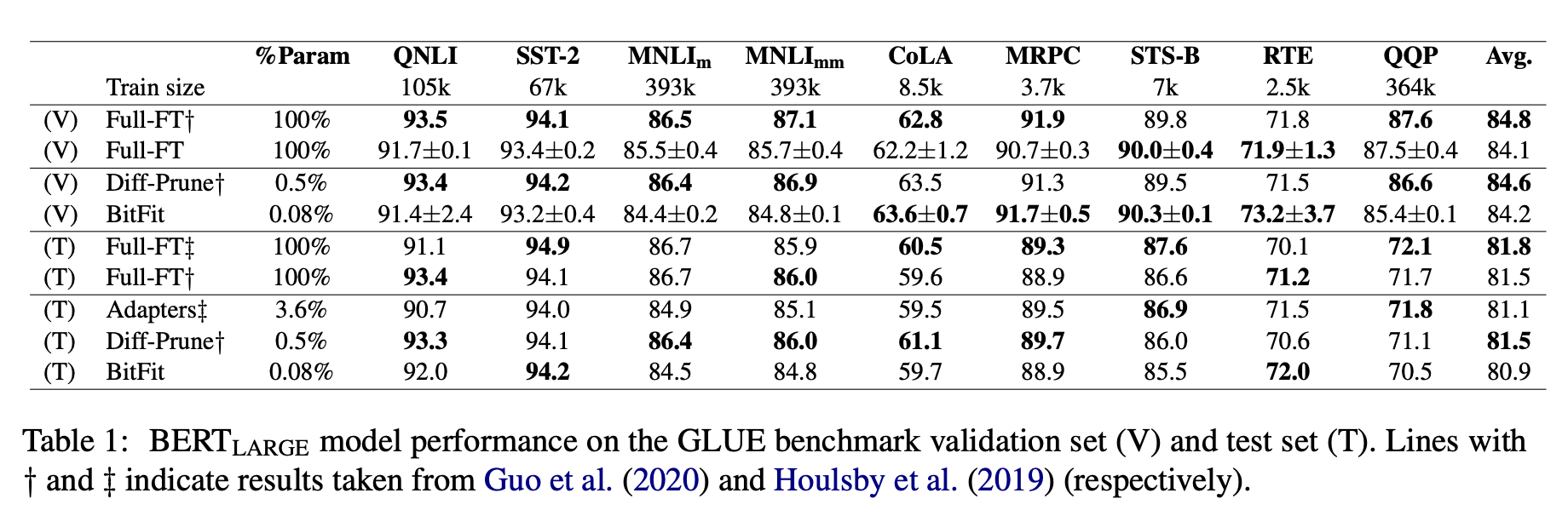
作者把此方法应用到三个模型上都能收获到与全参数微调相近的精度。

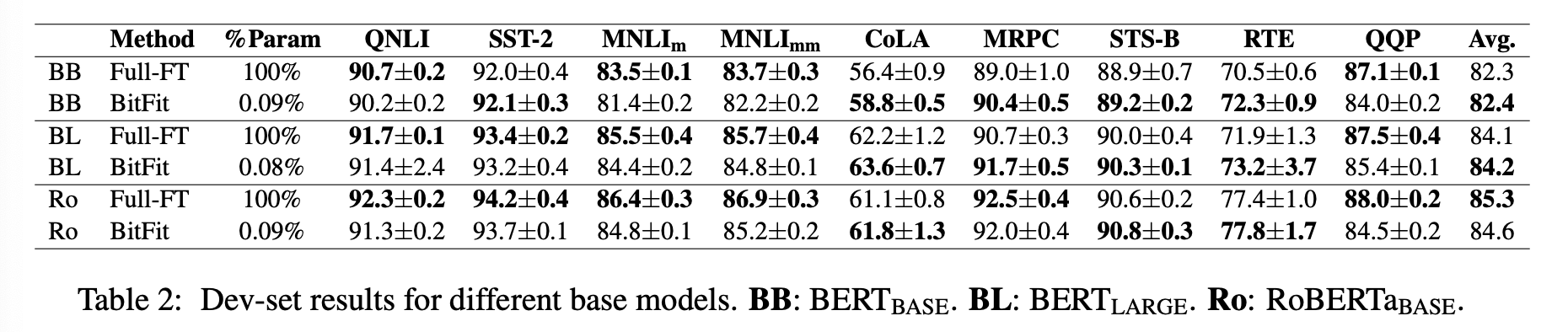
那偏置项有什么特殊吗？是不是从整个模型中随便选择相同体量的参数都能达到近似的精度？作者的实验表明相较于随机选择还是会有几个点的差别的。同时微调$b_q^{(·)}$和$b_{m2}^{(·)}$也能取得和微调所有$b$类似的精度。

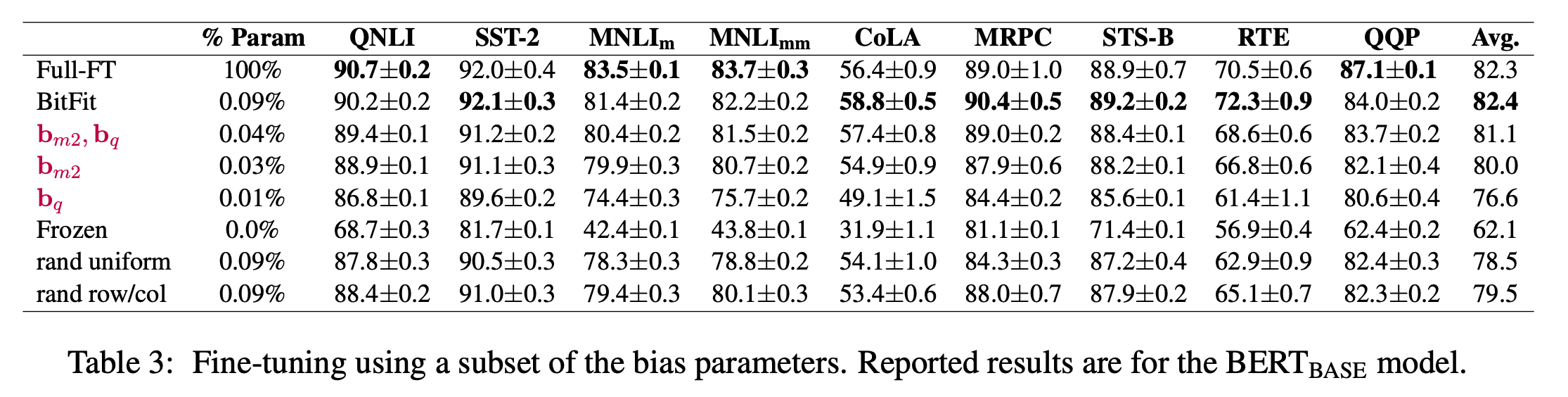
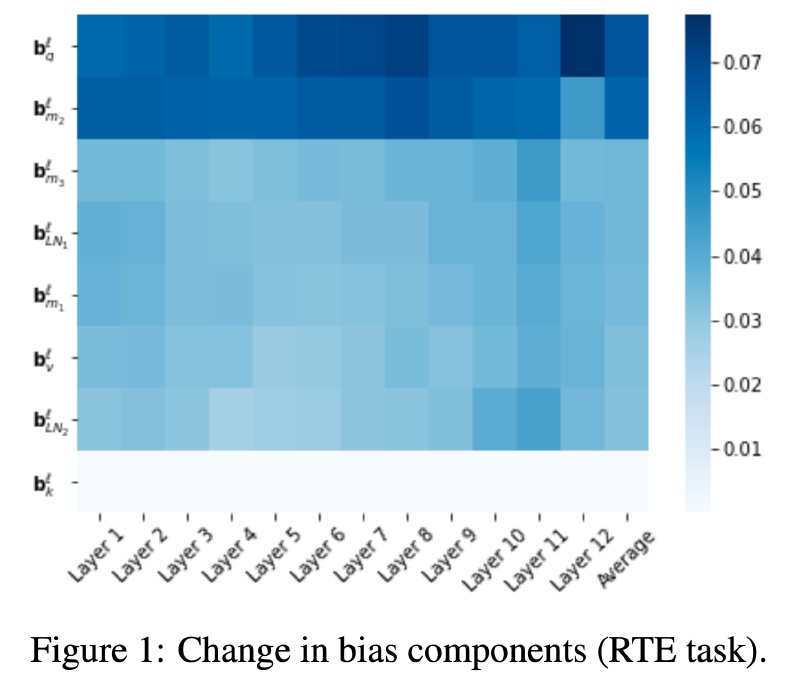
那么怎么发现$b_q^{(·)}$和$b_{m2}^{(·)}$的特殊性的呢？其实就是算改变量$\frac 1{dimb}||b_0-b_F||1$，$b_0$是初始权重，$b_F$是微调后的权重，可以看到$b_q^{(·)}$和$b{m2}^{(·)}$微调前后的改变量最大。

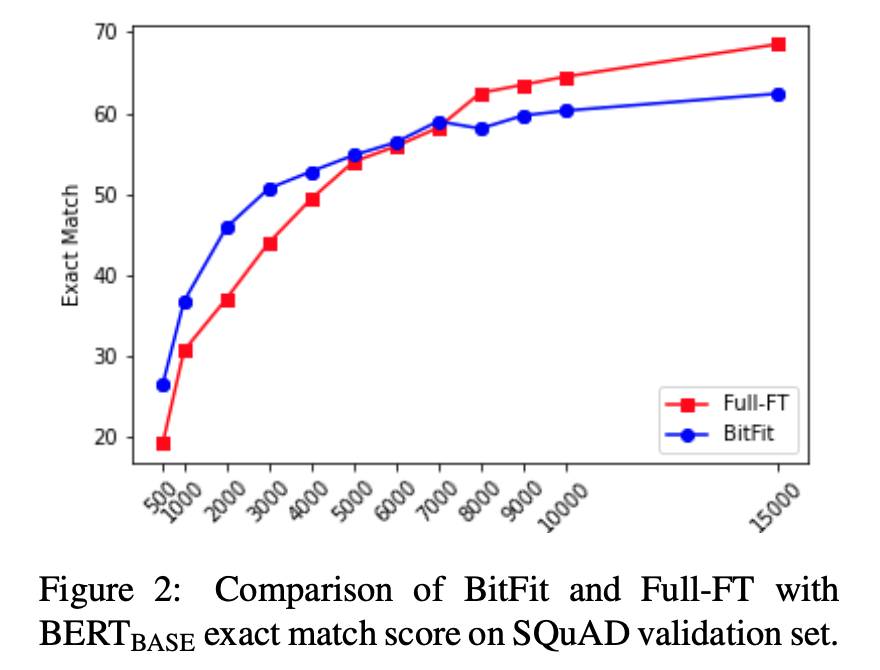
那模型效果上，真的是BitFit还能比全参数微调还好吗？实验发现这和微调的数据量有关，只要微调的数据量上来了，那全参数的效果还是更好的，当然，不止BitFit，其他微调方法也有这一问题。