先按照顺序列一下这几篇技术首次提交到arxiv的时间,我们按照提交时间来介绍,很多博客都搞不清楚发表时间,甚至把这几种方法张冠李戴,我们还是从原始信息源头进行梳理,这样虽然慢但是可靠。
论文:Adapter: Parameter-Efficient Transfer Learning for NLP 代码:Adapter 时间:2019.2.2
论文:Prefix-Tuning: Optimizing Continuous Prompts for Generation 代码:Prefix-Tuning 时间:2021.01.01
论文:P-tuning: GPT Understands, Too 代码:P-Tuning 时间:2021.03.18
论文:The Power of Scale for Parameter-Efficient Prompt Tuning 代码:Prompt Tuning 时间:2021.4.18
论文:LoRA: Low-Rank Adaptation of Large Language Models 代码:Lora 时间:2021.06.17
论文:BitFit: Simple Parameter-efficient Fine-tuning for Transformer-based Masked Language-models 代码:BitFit 时间:2021.06.18
论文:P-Tuning v2: Prompt Tuning Can Be Comparable to Fine-tuning Universally Across Scales and Tasks 代码:P-Tuning v2 时间:2021.10.14
论文:T-Few: Few-Shot Parameter-Efficient Fine-Tuning is Better and Cheaper than In-Context Learning 代码:T-Few 时间:2022.04.11
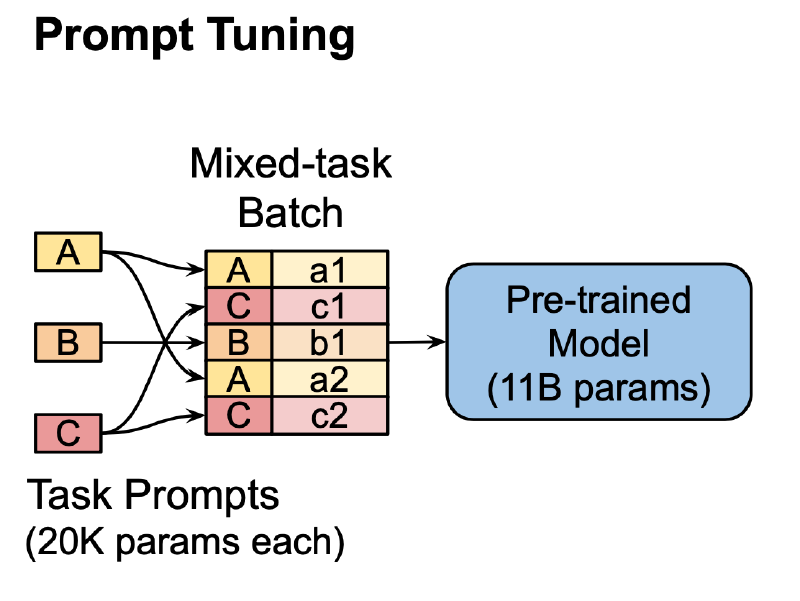
Prompt Tuning
这篇文章终于提到了前面的工作也就是Prefix-Tuing,可以说Prompt Tuning相当于一个更简单的版本Prefix-Tuing,本文实验验证了当模型越来越大时,Prompt Tuning的效果要比微调模型的效果更好,在领域外的问题上,Prompt Tuning不会像微调模型一样把模型弄傻掉。
下面介绍具体做法,还是用作者定义的公式来说明吧,LLM工作的原理可以表示为$Pr_\theta(Y|X)$,也就是在输入$X$的情况下,使用网络参数$\theta$,计算输出$Y$的概率。
prompt可以表示为一系列预先添加的token,用$P$表示,所以现在过程变成了$Pr_\theta(Y|[P;X])$。尝试只优化$P$来优化模型,其中$P = {p_1, p_2, . . . , p_n}$。这个$P$其实也是用了部分网络参数$\theta$得到的,因为它来自于LLM中的embeding层,选择不同的token id输入到embedding层,就能构造出不同的$P$。
之前的手动选择prompt的方法和一些不可微的prompt搜索方法,都有$P$来自embeding层的这个限制,这篇文章就是把这个限制给拿掉。
说的更简单点,之前的方法都是尝试从embedding层中根据token id挑选一些行来作为$P$,embeding本身是冻结的。但是prompt tuning的$P$则是自己学习到的,不要求其必须来源自embeding。对于按照我们博客顺序读下来的作者,这点其实早就明白了,因为prefix-tuning以及p-tuning都是这样做的,甚至读到这里我感觉它和P-Tuning没有任何本质差别,这几个可以视为同期工作,而这里提到的以前的方法,可能说的是2019或者2020的方法。
再用公式化说明确点,本文方法接收n个token作为输入${x_1,x_2,..,x_n}$,通过embeding层得到$X_e$,它的大小为$n \times e$,$e$是嵌入层的特征长度。本文学习到的软prompt可以表示为$P_e$,它的大小是$p \times e$,$p$是软token的长度,最后把$P_e$和$X_e$结合在一起,作为LLM的输入,优化loss来微调$P_e$,实现精度的提升。
与P-Tuning的差别
读到这里,大家应该都会比较疑惑了🤔,这和P-Tuning有啥区别呀,先来说说Prompt Tuning的做法:
Prompt Tuning其实可以随机初始化软Prompt也就是$P_e$,但最后选择的做法是先找几个token id 到embding中取值来作为$P_e$的初始化,然后优化$P_e$。
P-Tuning更复杂一点,它也是有个软Prompt,这部分也可以用上面说的初始化方法,但是P-Tuning不是直接用的这个软Prompt与输入拼接起来,而是用一个全连接层或者lstm对这个软prompt给变化了一下,再与输入拼接起来,相当于本文的Prompt Tuning其实是P-Tuning的一个退化版本,而且P-Tuning还可以软硬prompt结合,看arxiv提交时间来看,Prompt Tuning比P-Tuning晚,不知道为什么还能发出来。
实验
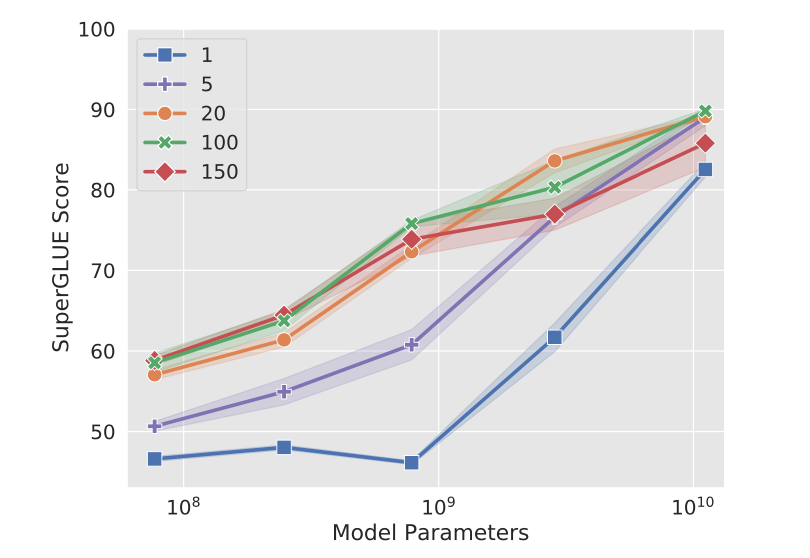
这篇文章做了几个实验说一下,一个是prompt长度对最后精度的实验,总结来说当模型大小一样的时候,prompt越长,微调后的精度也就越高。但是如果模型足够大,只使用一个prompt,精度也会很好。换言之,模型越来越大时,prompt长度的重要性越来越弱。
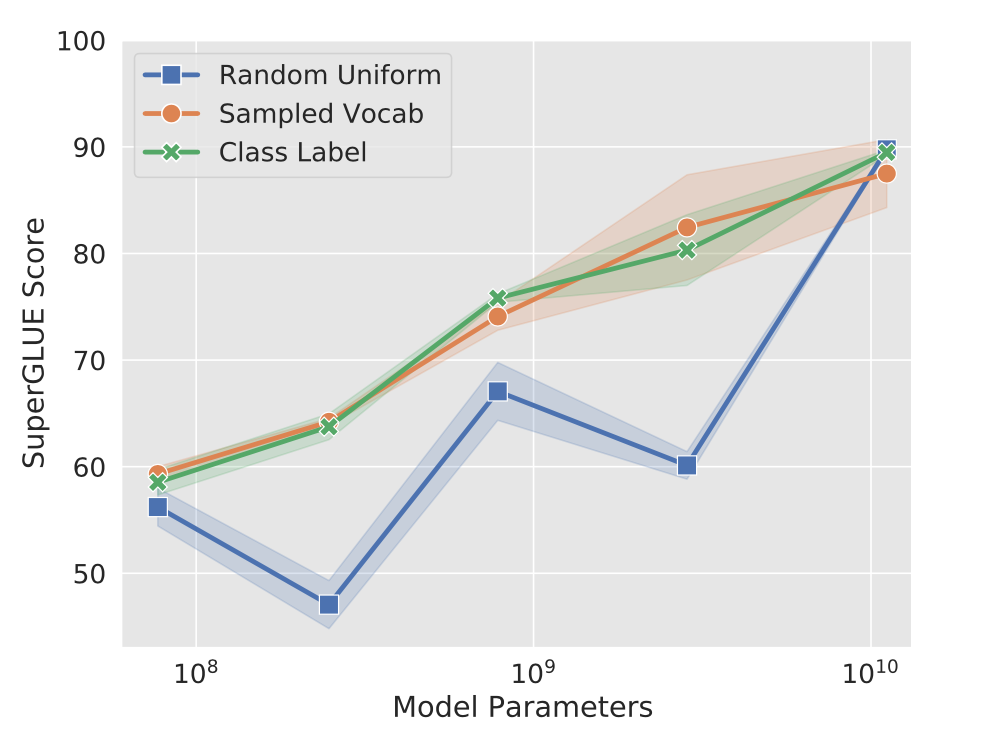
上文提到的初始化方式上也会对最终精度有显著影响,从词汇表也就是embeding初始化的效果要比随机初始化好。
本人挺不喜欢这个文章的,虽然提到了P-Tuning与Prefix Tuning,但是并未进行对比实验来验证精度差别,如果你们在哪里看到了可以在评论下面告诉我。