数学描述如下，A就是矩阵，$v$就是特征向量，$\lambda$就是特征值

$$ Av=\lambda v $$

化简一下就是：

$$ (A-I\lambda)v=0 $$

可以展开写为

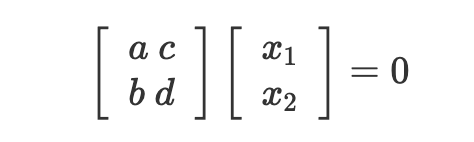
$$ \textstyle\left[{\begin{array}{l}{a\ c}\ {b\ d}\end{array}}\right]\left[\begin{array}{c}{{x_{1}}}\ {{x_{2}}}\\end{array}\right]=0 $$ (🤔这公式网页渲染不了,看上面图片吧)

也就是

$$ \begin{array}{c}{{a x_{1}\ +,c x_{2}=0\underline{{{}\underline{{{}}}}}}}\ {{b x_{1}\ +,d x_{2}=0}}\end{array} $$

这个方程有非零解，则需要

$$ {\frac{a}{c}}={\frac{b}{d}} $$

这个其实就是说这个矩阵两行其实是平行的，按照数学上的说法就叫不满秩

解$(A-I\lambda)v=0$，带入矩阵算一下得到：

$$ (a-\lambda)(d-\lambda)-bc=0 $$

这是个二维矩阵，所以特征值为$\lambda_1$和$\lambda_2$，也可以写为：

$$ (\lambda_1-\lambda)(\lambda_2-\lambda)=0 $$

非常数项一定要相等，所以：

$$ |A|=ad-bc=\lambda_1\lambda_2 \rightarrow|A|=\prod_{i}\lambda_{i} $$

其实就是说行列式的值等于特征值的乘积